Tensorflow Linear Regression

구글에서 발표한 머신러닝을 위한 오픈소스 라이브러리 입니다. 많은 머신러닝 서비스에서 사용 중이며, Python으로 개발이 가능해서 개발 접근성이 매우 좋습니다.

Linear Regression 이란?

선형 회귀는 y와 한 개 이상의 x가 선형 상관 관계를 모델링 하는 기법입니다. 말은 어렵지만 아래의 계산식을 보면 이해하기가 좋습니다.

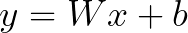
y의 답에 도달하기 위해 주어진 x가 있고, W(weight)의 값과 b(bias)의 값을 조정해서 결과적으로 y와 일치할 수 있도록 합니다.

횟수	y	x
1회	4	1
2회	5	2
3회	6	3
4회	7	4
5회	8	5

위와 같이 y, x의 값이 값이 있을 때 풀어보면 W = 1, b = 3 이라는 결과가 나옵니다. 이렇게 결과값이 나올 수 있도록 y, x의 관계를 정리해서 추론한 것이 Linear Regression 입니다.~~(수학과가 아니라서 잘못 이해했을 수도 있습니다.)~~

방법은?

어디다 써먹지?

실제 코드로 해보자!

import tensorflow.compat.v1 as tf_v1

# x_train = 각 학생 별 공부 시간(시간)
# y_train = 최종 학생별 중간고사 점수
x_train = [10, 20, 30, 40]
y_train = [15, 33, 40, 80]

# W, b는 시작에서는 정확한 값을 모르기 때문에 random으로 처음 설정을 함
W = tf_v1.Variable(tf_v1.random_normal([1]), name="weight")
b = tf_v1.Variable(tf_v1.random_normal([1]), name="bias")

# 계산식 : H(x) = Wx + b
# 랜덤한 W, b를 가지고 계산해서 나오는 결과값을 H(x) 라고 한다
hypothesis = W * x_train + b

# cost/Loss function : 오차율 평균을 구하는 코드
# 랜덤으로 나온 W, b를 가지고 계산한 결과값인 H(x)와 실제 결과값 y를 뺀 후
# 제곱(square)을 해준다
# * 제곱을 하는 이유
#  1) 오차에 음수와 양수가 섞이게 되면 정확한 오차율이 나오지 않음
#  2) 확대 계산으로 오차율 보정을 효율적으로 하기 위해
# 위 내용으로 나온 값을 기반으로 합산하여 평균(reduce_mean)을 측정한다.
cost = tf_v1.reduce_mean(tf_v1.square(hypothesis - y_train))

# Gradient Descent Algorithm 으로 오차율을 감소 학습 진행을 위한 변수 선언
# 참고 : https://medium.com/@peteryun/ml-%EB%AA%A8%EB%91%90%EB%A5%BC-%EC%9C%84%ED%95%9C-tensorflow-3-gradient-descent-algorithm-%EA%B8%B0%EB%B3%B8-c0688208fc59
# learning_rate 는 오차 보정 시 움직일 스탭의 단위(작으면 작을 수록 미세조정이 가능 다만 횟수가 늘어나야 안정적이 되는것 같음)
# 0.1 정도로 했을 때는 오차율이 너무 높아져서 오류로 안되는 경우도 발생
optimizer = tf_v1.train.GradientDescentOptimizer(learning_rate=1e-5)

# 학습 알고리즘을 적용한 변수 선언
train = optimizer.minimize(cost)

# Tensorflow 기능 수행을 위해 필요한 기본 Session
session = tf_v1.Session()
# Variable 사용 시 꼭 선언 필요
session.run(tf_v1.global_variables_initializer())

# 2000번 학습 진행
for step in range(2001):
    session.run(train)

		# 100번 마다 진행 상황 공유
    if step % 100 == 0:
        print("Step: ", step, "Loss : ", session.run(cost), "W : ", session.run(W), "b : ", session.run(b))

# 학습된 데이터셋을 활용 35 시간 공부 시 예상점수 표출 
print("당신의 예상 점수는 " + str(session.run(hypothesis, feed_dict={X: [[35.]]})))
# 당신의 예상 점수는 [[60.50574]] - 거의 비슷하게 나올듯

# Hypothesis : H(x)라고도 하며 y, x의 관계를 정의하는 가설이 된다.
# Cost Function : (or Loss) 결과값의 오차율을 확인

위 코드를 실행해보면 결과적으로 y값을 도출할 수 있는 학습셋(hypothesis, H(x))이 만들어지고 해당 H(x)을 가지고 x값을 대입해서 y값을 추출 합니다.

아직 초기 학습 단계라서 이제부터 1개씩 학습을 해나가면서 올릴 수 있도록 하겠습니다. 혹시라도 틀린 부분이 있다면 이야기 부탁드립니다 :)

Tensorflow 란?

Linear Regression 이란?

방법은?

어디다 써먹지?

실제 코드로 해보자!